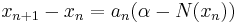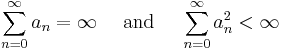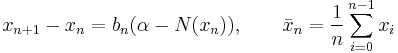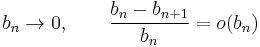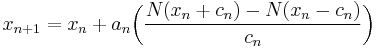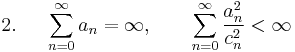Stochastic approximation

Stochastic approximation methods are a family of iterative stochastic optimization algorithms that attempt to find zeroes or extrema of functions which cannot be computed directly, but only estimated via noisy observations.

Mathematically, this refers to solving:

$\min_{x \in \Theta}\; f(x) = \mathbb E[F(x,\xi)]$

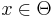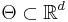where the objective is to find the parameter $x \in \Theta$ , which minimizes $f(x)$ for some unknown random variable, $\xi$ . Denoting $d$ as the dimension of the parameter $x$ , we can assume that while the domain $\Theta \subset \mathbb R^d$ is known, the objective function, $f(x)$ , cannot be computed exactly, but instead approximated via simulation. This can be intuitively explained as follows. $f(x)$ is the original function we want to minimize. However, due to noise, $f(x)$ can not be evaluated exactly. This situation is modeled by the function $F(x,\xi)$ , where $\xi$ represents the noise and is a random variable. Since $\xi$ is a random variable, so is the value of $F(x,\xi)$ . The objective is then to minimize $f(x)$ , but through evaluating $F(x,\xi)$ . A reasonable way to do this is to minimize the expectancy of $F(x,\xi)$ , i.e., $\mathbb E[F(x,\xi)]$ .

The first, and prototypical, algorithms of this kind are the Robbins-Monro and Kiefer-Wolfowitz algorithms.

1 Robbins–Monro algorithm
- 1.1 Complexity Results
- 1.2 Subsequent Developments
2 Kiefer-Wolfowitz algorithm
- 2.1 Subsequent Developments and Important Issues
3 Further Developments in Stochastic Approximation
4 See also
5 References

Robbins–Monro algorithm

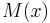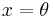The Robbins–Monro algorithm, introduced in 1951 by Herbert Robbins and Sutton Monro,^[1] presented a methodology for solving a root finding problem, where the function is represented as an expected value. Assume that we have a function $M(x)$ , and a constant $\alpha$ , such that the equation $M(x) = \alpha$ has a unique root at $x=\theta$ . It is assumed that while we cannot directly observe the function 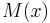$M(x)$ , we can instead obtain measurements of the random variable 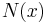$N(x)$ where $\mathbb E[N(x)] = M(x)$ . The structure of the algorithm is to then generate iterates of the form:

$x_{n%2B1}-x_n=a_n(\alpha-N(x_n))$

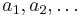Here, $a_1, a_2, \dots$ is a sequence of positive step sizes. Robbins and Monro proved ^[1]^{, Theorem 2} that 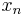$x_n$ converges in 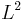$L^2$ (and hence also in probability) to $\theta$ provided that:

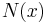$N(x)$ is uniformly bounded,
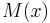$M(x)$ is nondecreasing,
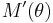$M'(\theta)$ exists and is positive, and
The sequence 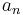$a_n$ satisfies the following requirements:

$\qquad \sum^{\infty}_{n=0}a_n = \infty \quad \mbox{ and } \quad \sum^{\infty}_{n=0}a^2_n < \infty \quad$

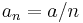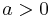A particular sequence of steps which satisfy these conditions, and was suggested by Robbins–Munro, have the form: $a_n=a/n$ , for $a > 0$ . Other series are possible but in order to average out the noise in 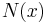$N(x)$ , the above condition must be met.

Complexity Results

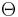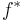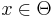If $f(x)$ is twice continuously differentiable, and strongly convex, and the minimizer of $f(x)$ belongs to the interior of $\Theta$ , then the Robbins-Monro algorithm will achieve the asymptotically optimal convergence rate, with respect to the objective function, being $\mathbb E[f(x_n) - f^*] = O(1/n)$ , where $f^*$ is the minimal value of $f(x)$ over $x \in \Theta$ .^[2]^[3]
Conversely, in the general convex case, where we lack both the assumption of smoothness and strong convexity, Nemirovski and Yudin ^[4] have shown that the asymptotically optimal convergence rate, with respect to the objective function values, is 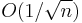$O(1/\sqrt{n})$ . They have also proven that this rate cannot be improved.

Subsequent Developments

While the Robbins-Monro algorithm is theoretically able to achieve 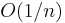$O(1/n)$ under the assumption of twice continuous differentiability and strong convexity, it can perform quite poorly upon implementation. This is primarily due to the fact that the algorithm is very sensitive to the choice of the step size sequence, and the supposed asymptotically optimal step size policy can be quite harmful in the beginning.^[3]^[5]

To overcome this shortfall, Polyak and Juditsky,^[6] presented a method of accelerating Robbins-Monro through the use of longer steps, and averaging of the iterates. The algorithm would have the following structure:

$x_{n%2B1} - x_n = b_n(\alpha - N(x_n)), \qquad \bar{x}_n = \frac{1}{n} \sum^{n-1}_{i=0} x_i$

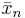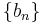The convergence of $\bar{x}_n$ to the unique root $\theta$ relies on the condition that the step sequence $\{b_n\}$ decreases sufficiently slowly. That is

$b_n \rightarrow 0, \qquad \frac{b_n - b_{n%2B1}}{b_n} = o(b_n)$

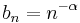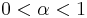Therefore, the sequence $b_n = n^{-\alpha}$ with $0 < \alpha < 1$ satisfies this restriction, but 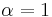$\alpha = 1$ does not, hence the longer steps. Under the assumptions outlined in the Robbins-Monro algorithm, the resulting modification will result in the same asymptotically optimal convergence rate 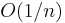$O(1/n)$ yet with a more robust step size policy.^[6]

Prior to this, the idea of using longer steps and averaging the iterates had already been proposed by Nemirovski and Yudin ^[7] for the cases of solving the stochastic optimization problem with continuous convex objectives and for convex-concave saddle point problems. These algorithms were observed to attain the nonasymptotic rate 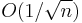$O(1/\sqrt{n})$ .

Kiefer-Wolfowitz algorithm

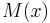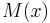The Kiefer-Wolfowitz algorithm,^[8] was introduced in 1952, and was motivated by the publication of the Robbins-Monro algorithm. However, the algorithm was presented as a method which would stochastically estimate the maximum of a function. Let $M(x)$ be a function which has a maximum at the point $\theta$ . It is assumed that $M(x)$ is unknown, however, certain observations 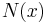$N(x)$ , where $\mathbb E[N(x)] = M(x)$ , can be made at any point $x$ . The structure of the algorithm follows a gradient-like method, with the iterates being generated as follows:

$x_{n%2B1} = x_n %2B a_n \bigg(\frac{N(x_n %2B c_n) - N(x_n -c_n)}{c_n} \bigg)$

where the gradient of 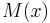$M(x)$ is approximated using finite differences. The sequence 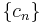$\{c_n\}$ specifies the sequence of finite difference widths used for the gradient approximation, while the sequence 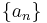$\{a_n\}$ specifies a sequence of positive step sizes taken along that direction. Kiefer and Wolfowitz proved that, if 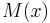$M(x)$ satisfied certain regularity conditions, then 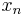$x_n$ will converge to $\theta$ provided that:

The function has a unique point of maximum (minimum) and is strong concave (convex)
- The algorithm was first presented with the requirement that the function 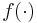$f(\cdot)$ maintains strong global convexity (concavity) over the entire feasible space. Given this condition is too restrictive to impose over the entire domain, Kiefer and Wolfowitz proposed that it is sufficient to impose the condition over a compact set 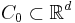$C_0 \subset \mathbb R^d$ which is known to include the optimal solution.
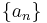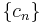The selected sequences $\{a_n\}$ and $\{c_n\}$ must be infinite sequences of positive numbers such that:

$\mbox{1. } \quad c_n \rightarrow 0, \quad a_n \rightarrow 0 \quad \mbox{ as } \quad n \rightarrow \infty$

$\mbox{2. } \quad \sum^\infty_{n=0} a_n = \infty, \qquad \sum^\infty_{n=0} \frac{a^2_n}{c^2_n} < \infty$

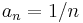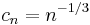A suitable choice of sequences, as recommended by Kiefer and Wolfowitz, would be $a_n = 1/n$ and $c_n = n^{-1/3}$ .

Subsequent Developments and Important Issues

The Kiefer Wolfowitz algorithm requires that for each gradient computation, at least 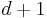different parameter values must simulated for every iteration of the algorithm, where is the dimension of the search space. This means that when is large, the Kiefer-Wolfowitz algorithm will require substantial computational effort per iteration, leading to slow convergence.
1. To address this problem, Spall, proposed the use of simultaneous perturbations to estimate the gradient. This method would require only two simulations per iteration, regardless of the dimension $d$ .^[9]
In the conditions required for convergence, the ability to specify a predetermined compact set that fulfills strong convexity (or concavity) and contains the unique solution can be difficult to find. With respect to real world applications, if the domain is quite large, these assumptions can be fairly restrictive and highly unrealistic.

Further Developments in Stochastic Approximation

An extensive theoretical literature has grown up around these algorithms, concerning conditions for convergence, rates of convergence, multivariate and other generalizations, proper choice of step size, possible noise models, and so on.^[10]^[11] These methods are also applied in control theory, in which case the unknown function which we wish to optimize or find the zero of may vary in time. In this case, the step size 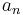$a_n$ should not converge to zero but should be chosen so as to track the function.^[10]^{, 2nd ed., chapter 3}

C. Johan Masreliez and R. Douglas Martin were the first to apply stochastic approximation to robust estimation.^[12]

References

^ ^a ^b A Stochastic Approximation Method, Herbert Robbins and Sutton Monro, Annals of Mathematical Statistics 22, #3 (September 1951), pp. 400–407.
^ Asymptotic distribution of Stochastic Approximation, J. Sacks, Annals of Mathematical Statistics 29, (1958), pp. 373–409.
^ ^a ^b Robust Stochastic Approximation Approach to Stochastic Programming, A. Nemirovski, A. Juditsky, G. Lan and A. Shapiro, SIAM Journal of Optimization 19, (January 2009), No. 4. pp. 1574–1609.
^ Problem Complexity and Method Efficiency in Optimization, A. Nemirovski and D. Yudin, Wiley -Intersci. Ser. Discrete Math 15 John Wiley New York (1983) .
^ Introduction to Stochastic Search and Optimization: Estimation, Simulation and Control, J.C. Spall, John Wiley Hoboken, NJ, (2003).
^ ^a ^b Acceleration of Stochastic Approximation by Averaging, B.T. Polyak and A.B. Juditsky, SIAM Journal on Control and Optimization 30, (July 1992) No. 4. pp. 838-855.
^ On Cezari's convergence of the steepest descent method for approximating saddle points of convex-concave functions, A. Nemirovski and D. Yudin, Dokl. Akad. Nauk SSR 2939, (1978 (Russian)), Soviet Math. Dokl. 19 (1978 (English)).
^ Stochastic Estimation of the Maximum of a Regression Function, J. Kiefer and J. Wolfowitz, Annals of Mathematical Statistics 23, #3 (September 1952), pp. 462–466.
^ Adaptive Stochastic Approximation by the Simultaneous Perturbation Method, James C Spall, IEEE Transactions on Automatic Control 45, #10 (October 2000), pp. 1839–1853.
^ ^a ^b Stochastic Approximation Algorithms and Applications, Harold J. Kushner and G. George Yin, New York: Springer-Verlag, 1997. ISBN 038794916X; 2nd ed., titled Stochastic Approximation and Recursive Algorithms and Applications, 2003, ISBN 0387008942.
^ Stochastic Approximation and Recursive Estimation, Mikhail Borisovich Nevel'son and Rafail Zalmanovich Has'minskiĭ, translated by Israel Program for Scientific Translations and B. Silver, Providence, RI: American Mathematical Society, 1973, 1976. ISBN 0821815970.
^ R.D. Martin & C.J. Masreliez, Robust estimation via stochastic approximation. IEEE Trans. Inform. Theory, 21(pp.263—271) (1975).